Happy New Year! Welcome to “Professor’s Corner” for 2023! And a special welcome to those readers who are new to the exciting field of UV/EB polymerization. If you are just beginning to read UV+EB Technology, let me encourage you to find back copies of the magazine to review all 16 of the previous editions of this column. Each new article is given meaningful context by all the previous articles, with the first article in 20191 providing three objectives for the column as well as a brief introduction to polymer science.
I want to express my appreciation to Dr. Mike Idacavage for providing an excellent article entitled, “Adhesion and Energy-Curable Coatings” for the last issue of “Professor’s Corner.”2 I hope to have other guest columnists providing discussions of special topics in the future.
Free Radical Polymerization Kinetics
With the noted exception of thiol-ene photopolymerization – a free-radically initiated “step-growth” polymerization process – UV/EB polymerization involves chain-growth polymerization kinetics. This includes both free radical and cationic processes. In this edition of Professor’s Corner, an introduction to free radical polymerization kinetics will be presented. This field of polymer science is concerned with the rate or “speed” of polymerization reactions and the factors that affect the rate. A study of kinetics leads to the development of proposed reaction mechanisms that explain how reactants move, step-by-step, toward products at the molecular scale. It is important to note, however, that reaction mechanisms are formal hypotheses which may be demonstrated to be incorrect with subsequent experimentation. They can be disproven but never actually proven in the conventional sense.
A well-established mechanistic hypothesis for free radical polymerization involves at least three steps or phases: Initiation, Propagation and Termination. Some specific reactions also may involve a fourth step: Chain-Transfer. Let’s deal with each of these phases in sequence.
Initiation – The initiation process for free radical polymerization involves a “radical generation” step and a subsequent “polymer initiation” step. Reactions 1 and 2 represent these two steps, respectively. In these reactions, “I” represents the initiator, “R.” represents the free radical, “M” represents a monomer (or oligomer) and “M1.” represents a new radical after initiation. The “k” values are the rate constants for decomposition of the initiator and for the initiation reaction, respectively. The radical generation step is the slowest step in the process and is called the “Rate Determining Step” (RDS). Therefore, it determines the overall rate of the initiation process. With these reactions, we can write a mathematical description for the rate of the reaction (Equation 1).
Equation 1 is a differential equation that shows that the rate of the initiation is directly proportional to the initiator concentration. The proportionality constant, in this case, is 2fkd where “f” is the relative efficiency of the initiator. That is, the ratio of the radicals that initiate a growing polymer chain to the total radicals generated. The efficiency of free radical initiators, according to Stevens3, usually is 0.3 < f > 0.8. The factor of “2” in the equation represents the fact that two radicals are formed during the radical generation step. Equation 1 shows that when the initiator concentration in increased, the rate of initiation increases proportionally.
Propagation – The kinetic expression of the propagation phase of the mechanism assumes that the rate constant, kp, is the same, regardless of the length of polymer chain to which it is attached. This is a reasonable assumption since, within the body of the reaction mixture, every growing chain’s free radical is surrounded by monomer molecules, making rapid bimolecular collision inevitable. Reactions 3 through 6 provide a few of the many steps in polymer propagation.
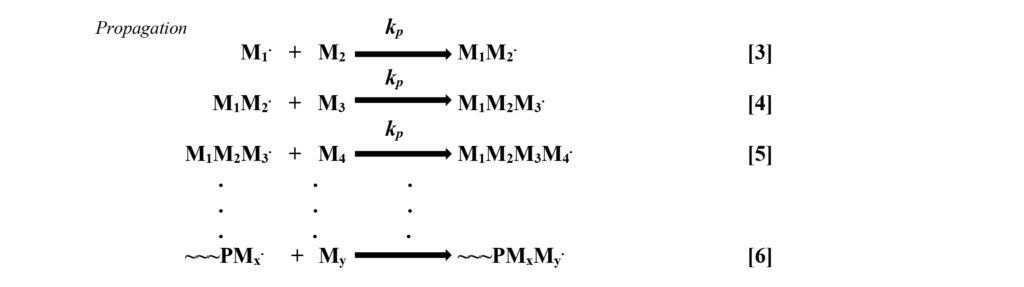For reactions to occur, there must be collisions among the reactive species, each of which must have proper orientation, and sufficient energy must be present for the reaction to occur. Since the relatively small monomer molecules are in direct contact with the growing chain ends and free radical polymerization is exothermic, the three conditions for reaction are present and rapid reaction occurs. Equation 2 gives the rate expression for propagation. It shows that the rate of decrease in monomer concentration is proportional to the product of the concentration of growing chain radicals and the monomer concentration. Increasing either of these will increase the rate of the reaction. Note: The rate of propagation essentially is the rate of polymerization.
Termination – The free radicals on the ends of the growing chains in the propagation phase of the mechanism are single unpaired electrons. When these encounter another unpaired electron, termination occurs with a single bond being formed between the two reacting species. These termination reactions can happen either by direct combination of two free radicals or through a process of disproportionation. Reactions 7 and 8 illustrate these two types of terminations.
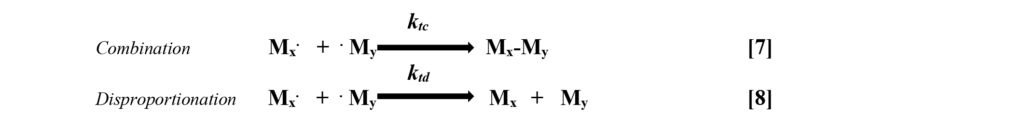Disproportionation involves the transfer of a hydrogen atom from one growing chain to the other. The hydrogen atom with its one electron (H.) then terminates the receiving chain. The breaking of the H-C bond on the other chain leaves behind an electron that then combines with the carbon-centered electron to form a terminal double bond. Thus, two growing chain radicals are terminated, and two macromolecules are formed. The double-bonded species can then, potentially, react with another free radical that happens to collide with it. These elementary steps in the mechanism provide the mathematical expression (Equation 3) for the rate of termination. This equation shows that the rate of termination is proportional to the square of the concentration of free radical growing chains.
Steady State Assumption – In free radical polymerization, the rate constants for termination (kt) are significantly larger than the rate constants for initiation (kd). This means that soon after the reaction begins, radical terminations occur as rapidly as radical formations and the concentration of radicals then becomes constant. This is the steady state assumption. It allows for a simple solution to the differential equations by setting the rate of initiation equal to the rate of termination as shown in Equation 4.
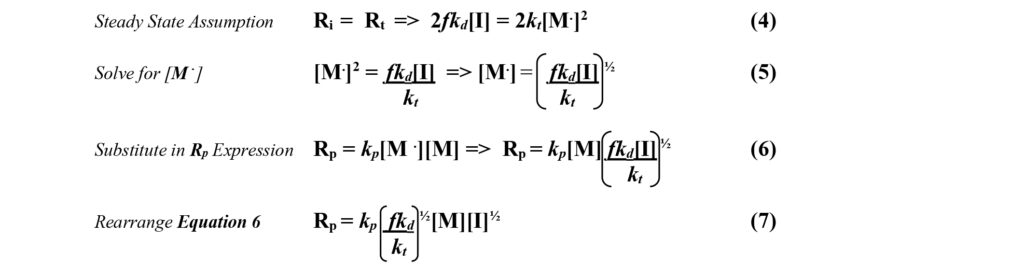Equation 7 shows that the rate of free radical polymerization is proportional to the product of the monomer concentration and the square root of the initiator concentration. Raising the concentration of either of these reactants will cause an increase in the rate of the polymerization reaction.
For more detailed information about the kinetics of free radical polymerization processes, see Reference 4.
References
- Christmas, Byron K., “Professor’s Corner”, UV+EB Technology, Vol. 5, No. 1, 2019, pp. 14-15.
- Idacavage, Mike J., “Adhesion and Energy-Curable Coatings”, UV+EB Technology, Vol. 8, No. 4, 2022, pp. 14-15.
- Stevens, Malcolm P., Polymer Chemistry: An Introduction, Oxford Univeristy Press, 1999, pg. 179.
- Christmas, Byron K. & Idacavage Mike J., Photopolymerization: Fundamental Polymer Science & Indusrial Applications, DEStech Publications, Inc., 2023, pp. 54-60.
Byron K. Christmas, Ph.D.
Professor of Chemistry, Emeritus
University of Houston-Downtown
b4christmas@gmail.com
