by Stephen C. Lapin, PCT Engineered Systems LLC
Question: What are the Fundamental Differences Between UV and EB Technology?
Answer: Ultraviolet (UV) and electron beam (EB) curing technologies are often grouped together. This is certainly the case in this new publication, UV+EB Technology. The main reason the technologies are considered together is that UV and EB energy can be used to initiate rapid polymerization of monomers and oligomers. This process is often referred to as “radiation curing” or “energy curing.” This similarity is well known, but it is much less common to ask how UV and EB technologies are different.
Perhaps the best way to understand the difference is to consider the fundamentals of UV and EB energy. Photons are the smallest “bit” of UV energy. They are considered by physicists to have properties of both a particle and a wave. Photons do not have mass. The energy of a photon is determined by its wavelength. Most UV-curing chemistry uses wavelengths from about 250 to 450 nm.
The smallest “bit” of EB energy is the electron. Unlike photons, electrons have mass and they are negatively charged. The energy of electrons is determined by the voltage potential used in the acceleration process. For curing applications, we are most often using equipment that accelerates electrons in the range of about 70 to 300 kV. The behavior of the electron beam is best characterized as accelerated particles rather than a form of electromagnetic radiation.
Simple conversion of energy units shows that a 350 nm UV photon is equivalent to 3.5 eV. This is in contrast to electrons accelerated at 110 kV. The electrons slow somewhat as they pass through the window foil and air gap but still average on the order of 70,000 eV when they reach the substrate. This means that EB electrons are on the order of 20,000 times more energetic than UV photons! If one considers that a typical C-H or C-C bond energy is on the order of 4 to 5 eV, then it becomes clear that EB has more than enough energy to break chemical bonds. This bond-breaking ability qualifies EB as a form of “ionizing radiation” as compared to UV, which is “non-ionizing.” The bond-breaking power of EB is why free radical curing occurs without an added photoinitiator. The radicals can form directly by EB acting on the monomer and oligomer portion of the compositions.
Given this discussion of the energy of individual photons and electrons, how does the total amount of energy applied in the curing process compare for UV and EB? Applied UV energy is usually given as energy per unit area in units of mJ/cm2 or J/cm2. Applied EB energy is given in energy per unit mass in units of Mrads or kGy. By definition, 1 kGy = 1 J/gram. The applied energy for UV curing can vary widely depending on the application but is often in the range of 0.1 to 0.5 J/cm2. A typical EB cure dose for curing acrylate-based chemistry is usually in the range of 20 to 40 kGy. Assuming that this EB energy is deposited in a 50 g/m2 layer, then this equates to an applied energy of 0.1 to 0.2 J/cm2 at the surface. It is interesting that the total energy applied for UV and EB can be quite similar in spite of the individual “bits” being so different.
Another fundamental difference between UV and EB energy is the manner by which the energy is deposited into the materials to be cured or treated. This is very critical because curing only occurs where the energy is deposited. (There are some special “shadow curing” chemistries that could be an exception to this statement.) UV energy deposition is determined by the optical density of the material. UV curing can occur quite deep (multiple inches) into clear materials where there is limited absorbance of the base material in competition with the photoinitiators.
In contrast, UV curing can be quite limited into opaque materials with a high optical density. High power, well focused (high peak irradiance) UV sources can be helpful to a degree in getting penetration in high optical density materials. The well-known relationship for predicting UV penetration into materials is the Bouguer-Lambert Law.
EB energy deposition does not depend on the optical density of the material. It penetrates equally well into clear and opaque materials. Instead, the mass density is a much better predictor of EB energy deposition into materials. Electrons are very small particles with a rest mass of about 5.5 x 10-4 AMU. A carbon nucleus is about 22,000 more massive than an electron. An analogy for electron penetration is in some ways like shooting BBs at a bowling ball. What makes EB penetration possible is the fact that condensed matter (liquids and solids) have a lot of space between the nuclei.
Electron beam penetration then becomes a matter of probability of avoiding a direct collision with a nucleus. Electron beam energy deposition in materials can be predicted by Monte Carlo calculations which, as the name implies, is a statistical averaging of the interactions of a large number of electrons. The interactions of accelerated electrons with matter were derived by physicists at collaborating National Laboratories more than 30 years ago. These were incorporated in powerful software programs that are available for industrial applications.
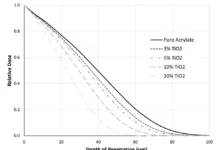
The inputs into Monte Carlo simulations are the elemental composition of the material and the accelerating voltage of the beam. Higher atomic number compositions are more effective at stopping the beam. Atomic number also is directly related to the density of a material, thus the correlation between density and EB penetration. The highly accurate Monte Carlo predictions can be verified by EB irradiation of stacks of radiochromic film dosimeters. A set of depth/dose cures for EB energy deposition in a polymer is shown in a subsequent article (see Figure 3 on page 46).

Figure 1 on page 10 helps to illustrate the difference between UV and EB energy deposition in materials. With UV, there are a large number of relatively low energy photons. The energy of the photons is concentrated at the surface and decreases exponentially though the material as predicted by Bouguer-Lambert Law. Longer wavelength photons may be less strongly absorbed and have enough penetration to cure through the material. With EB, there is a smaller number of higher energy electrons. Each electron may result in multiple initiating events. Given a selection of accelerating voltage appropriate for the material, the EB energy can be very uniform from the front to back surface of the material.
Hopefully this introduction provides a basis to explore EB application-related questions for future columns.
Stephen C. Lapin, Ph.D., is a BroadBeam applications specialist at PCT Engineered Systems LLC. He can be reached at sclapin@teampct.com.
Topic Suggestions
Do you have a question that you’d like to see addressed here? Submit your ideas for consideration to sclapin@teampct.com.